Exercise
Solve the square inequality:
4x^2-12x\geq -10
Final Answer
Solution
4x^2-12x\geq -10
Move everything to one side:
4x^2-12x+10\geq 0
It is a square inequality. its coefficients are
a=4, b=-12, c=10
The coefficient of the squared expression (a) is positive, so the parabola (quadratic equation graph) “smiles” (= bowl-shaped). The sign of the inequality means we are looking for the sections the parabola is above the x-axis. We find the solutions (= zeros = roots) of the quadratic equation using the quadratic formula. Putting the coefficients in the formula gives us
x_{1,2}=\frac{12\pm \sqrt{{(-12)}^2-4\cdot 4\cdot 10}}{2\cdot 4}=
=\frac{12\pm \sqrt{-16}}{8}
We got a negative number inside the root, so there is no real solution to the quadratic equation, i.e. its graph does not pass through the x-axis. Because it is “smiling”, it is always above the x-axis. Hence, the solution of the inequality is all x.
The graph of the equation:
y=4x^2-12x+10
looks like this:
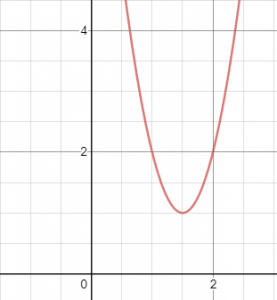
You can see that the graph is indeed above the x-axis for all x.
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!