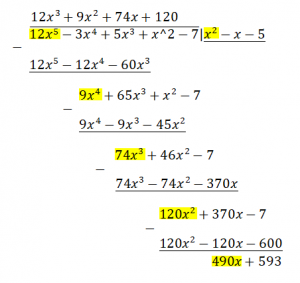Polynomial Long Division – Exercise 5664

Exercise

Do long division:

$\frac{12x^5-3x^4+5x^3+x^2-7}{x^2-x-5}$

Final Answer

Show final answer

Solution

Here is the long division:

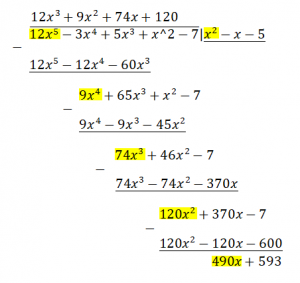
This is the result of the long division:

$\frac{12x^5-3x^4+5x^3+x^2-7}{x^2-x-5}$

$=(12x^3+9x^2+74x+120)+\frac{490x+593}{x^2-x-5}$

We can also present it like this:

$12x^5-3x^4+5x^3+x^2-7=$

$=(x^2-x-5)(12x^3+9x^2+74x+120)+(490x+593)$

Note:

$490x+593 \text{ is called the remainder.}$