Exercise
Determine the domain of the function:
f(x)=\sqrt{1-x^2}
Final Answer
Solution
Let’s find the domain of the function:
f(x)=\sqrt{1-x^2}
There is a square root, so we need the expression inside the root to be non-negative:
1-x^2\geq 0
It is a square inequality. The roots of the quadratic equation:
1-x^2=0
are
x_1=1, x_2=-1
Also, the coefficient of the square expression is negative (-1), so the graph looks like an inverted parabola (= inverted bowl = “crying”).
It looks like this:
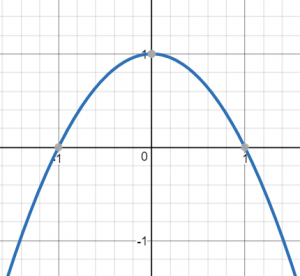
Back to inequality:
1-x^2\geq 0
We need to check when the equation we solved is not negative, i.e. when the graph is not below the x-axis. And one can see from the graph that this happens when the following holds
-1\leq x\leq 1
Have a question? Found a mistake? – Write a comment below!
Was it helpful? You can buy me a cup of coffee here, which will make me very happy and will help me upload more solutions!